私の若い頃のコンピュータといえば、ファミコンくらいのもので、今のようなインターネットや電子メールが一般的な時代ではなかった。
本格的にパソコンを自宅で使いだしたのは、20代後半からのことだったと記憶している。
あれから随分経つが、パソコンの機能は日々進化しているようである。
しかし、ごく基本的な事柄は何も変わってはいない。
今回は、コンピュータの基礎的な事柄について観てみたい。

コンピュータにおけるデータの表現
コンピュータの扱う整数、実数(自然数・0・負の整数・有限小数・循環小数・超越数でない無理数・超越数)、文字、画像、音声、プログラムなどといった情報は、いずれも0と1のみを利用した2進数で表現される。
また2進数以外に16進数なども利用される。
このようなn進数におけるnを基数という。
・基数変換
2進数から10進数への変換は以下の通りである。
1011.101=1×2³+0×2²+1×2¹+1×2⁰+1×2⁻¹+0×2⁻²+1×2⁻³=8+2+1+0.5+0.125=11.625
1の位には2の0乗をかけて、位が上がるごとに1乗、2乗・・と数値を上げていき、反対に0より下の位は、ー1乗、ー2乗・・と数値をマイナスしていき、各数値の合計が変換された10進数となる。
2進数1011.101は10進数11.625になるわけだ。
16進数から10進数への変換は、上の基数の2の部分を16に変えるだけだ。
10進数から2進数への変換では、整数部と小数部で少し違ってくる。
まずは整数部の変換である。
10進数の整数50を2進数で表現するには、50を基数2で割り算し、その商が0になるまで繰り返す。
商が0になった時点で、各割り算で得た余り(剰余)を逆順に並べると2進数に変換した結果が得られる。

図では、110010が得られる。ここで1を2で割ると0余り1になることに注意である。(簡単なようで案外難しい)
10進数の50は、2進数では110010という、いかにもコンピュータといった表現に変身するのだ!
整数だけ基数変換できても役には立たない。
次は、6.625を基数変換してみよう。
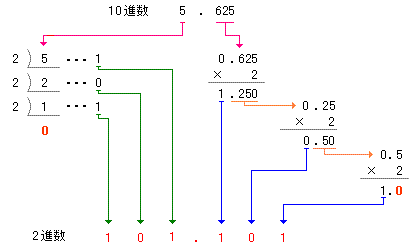
6は2で割り算していって算出した余り(剰余)から求められる。
余りを下から並べて101となる。
次に小数部分だが、こちらは整数部分とは反対に基数である2を乗じていく。
上の例だと、0.625に2をかけて1.250を算出した。
整数の1を除く0.250に再び2をかけて0.50を算出し、整数部分の0を除き、0.50に2をかけて1.00を算出する。
少数部分が0になったら終了する。
整数部分とは、これまた反対に上から並べて、.101となるのである。
10進数の5.625は、2進数では101.101となる。
小数部分の基数変換では、一点だけ注意が必要だ。
基数の2をかけていっても、いつも有限小数になるとは限らない。
例えば、10進数の0.7を2進数で表現しようとすると、いつまでたっても終了条件である0に到達しないのだ。

これを有限小数に対して無限小数という。
コンピュータの記憶領域は有限なので、有限長の2進小数で表現できない場合には、なるべく近い値で近似することになる。
この結果、誤差が生じることになる。
この無限に連続するような計算を有限の回数で打ち切るために生じる誤差を打切り誤差という。
上記の他に円周率(3.14・・・・)の計算なども挙げられる。
まとめると基数変換の要点は以下のとおりだ。
・整数部分の基数変換
割り算した余りを逆に並べる!
・小数部分の基数変換
掛け算した整数部分を順に並べる!
・負の数の表現方法
正の数値だけ表現できて、負の数値を表現できないのは片手落ちだろう。
固定桁(桁数が決められている)の2進数で負の数を表現する方法がある。
これは2の補数という考え方だ。
n桁の2進数kがあったとする。
基準値2ⁿからkを減じた数を2の補数というのである。
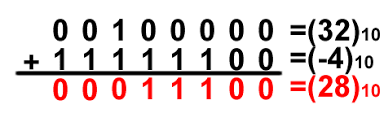
例をあげると、8桁の2進数(01001010)=74の2の補数は、基準値2⁸=256=(10000000)から(01001010)を減じた(10110110)となる。
これは、元の数kをビット反転した結果に1を加えた値と一致する。
二つの値を足して0になるということは、数字が同じでどちらかがマイナスにすれば0になるということであり、これにより負の数を表現しようというのである。

2の補数を用いることにより、n桁の2進数では(ー2ⁿ⁻¹)~(2ⁿ⁻¹ー1)の数を表現できる。
8桁の2進数だと、ー128から127を表現できるということだ。
また、2の補数では減算を加算で処理できる。例えば、8桁の2進数で32-4を計算する場合、4の2の補数を求めてから、32と(ー4)を加算すればよい。
・数値のデータ表現
コンピュータは、2進数の一桁の情報を最小単位であるビットに対応させて数値をデータとして表現する。
数値の表現方法は、固定小数点数、浮動小数点数などがある。
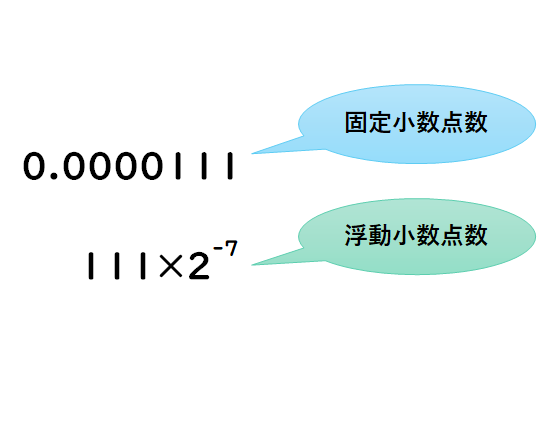
まずは、固定小数点数である。
固定小数点数とは、小数点の位置を固定して数値を表現する方式であり、主に小数点を右端に固定して整数を表現するのに用いられる。
正負を区別しない符号なし固定小数点数と、正負を区別する符号付き固定小数点数とがある。
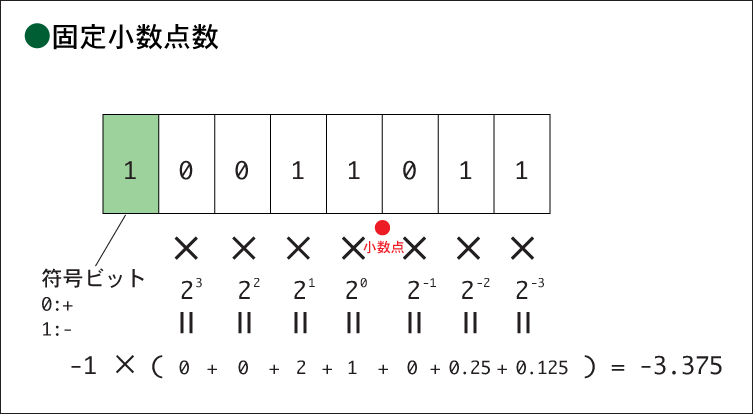
上図は符号付きの例である。
小数点の位置をコンピュータに覚えさせるのが特徴である。
表現できる数の範囲を下記に示そう。
| 方式 | 表現できる数の範囲 |
| nビットの符号なし固定小数点数 | 0〜2ⁿー1 |
| nビットの符号付き固定小数点数 | ー2ⁿ⁻¹~2ⁿ⁻¹-1 |
実は、この固定小数点数はコンピュータの世界ではあまり一般的ではない。
よく使われるのは、浮動小数点数の方である。
浮動小数点数は、実数を、仮数✖️基数^指数という指数表現で表す方式である。
コンピュータでは基数に2が用いられ、実数Xは次のように表現される。
X=(ー1)^ S× Ⅿ× 2^E
この式では、Mが仮数、Eが指数を表す。また、Sは符号を表し、Xが非負数のときは0に、負数のときは1となる。
浮動小数点数で表現する実数Xを10.5の2進数(1010.1)とすると、
10101.0×2^-1
1010.1×2^0
101.01×2^1
といった様々な指数表現が考えられる。
そこで、指数表現が一意となるようなルールを設定して、それに従って仮数と指数を調整する。これを正規化という。
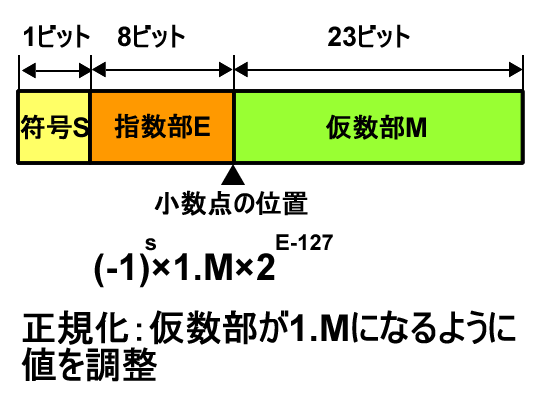
浮動小数点数を表現するための規格には、IEEEによって規格化されたIEEE単制度浮動小数点数などがある。
この方式では、上図のように、符号部、指数部、仮数部を次のように32ビットで表現する。
仮数部Mは、1<=仮数<2となるように正規化される。
よって、10.5の指数表現は 1.0101×2^3 となる。
仮数部の整数部分は常に1となるため、この1を表現する必要はない。そこで、小数部分のみを仮数部Mで表現する。
指数部には下駄履き表現(イクサス表現)が用いられる。これは、指数に一定の数を加えたものを指数部として表現する方法であり、IEEE単精度浮動小数点数であれば127が加えられる。
指数部の値から指数を得るには127を減じればよいのである。
この方法によって、指数は、
ー127(指数部Eが00000000)〜+128(指数部Eが11111111)
を表現できる。
例えば、−252.025 という実数を浮動小数点数で表現してみよう。
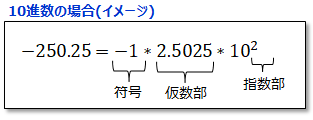

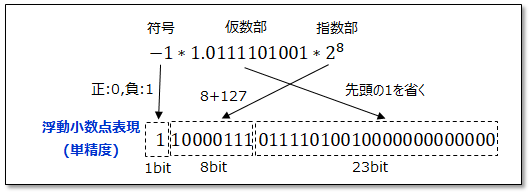
かなり複雑な姿に変貌してしまった!
・シフト演算
数値データに対する演算にシフト演算というものがある。
シフト演算とは、格納されたビットをシフトする(ずらす)演算であり、あふれたビットは捨てられ、空いたビットは0などの値で埋められる。
主に符号なし固定小数点数に用いられ、1のビットがあふれない限りは左にnビットした結果は元の数の2^n倍に、右にnビットシフトした結果は元の数の2^−n倍になる。
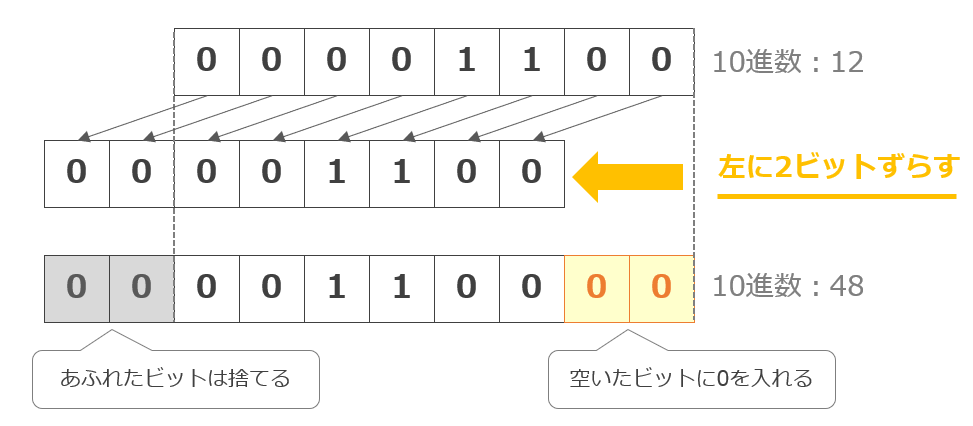
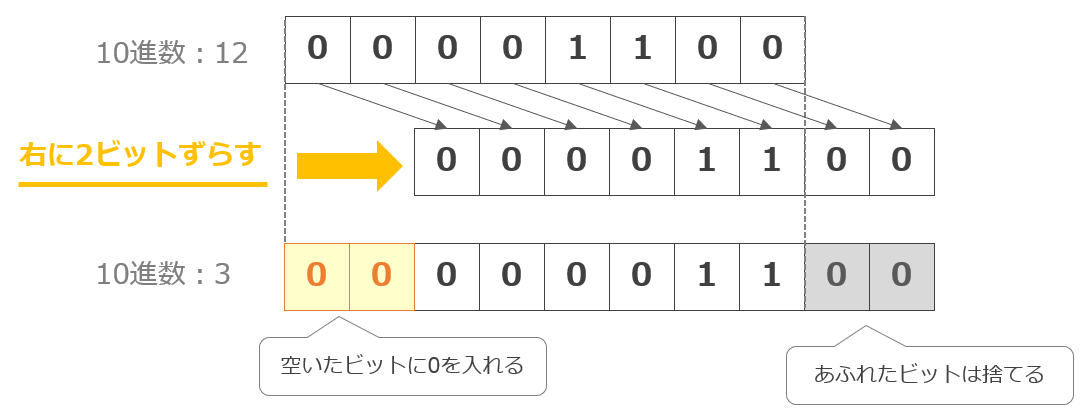
上図は、論理シフト演算といって正負の情報を意識せずに全ビットをシフトする演算であり、空いたビットは0で補われる。
これに対して、算術シフト演算というものがあり、正負を意味する最上位(左端)のビットはシフトの対象とはせずに、それ以外のビットを右に又は左に指定された数だけシフトする。
右シフトによって空いたビットには符号ビットと同じ符号を格納する点が論理シフト演算とは異なる。(左シフトで空いたビットには0を格納する)
算術シフト演算は、一般的には符号付き固定小数点数に用いられ、2の補数で表現された負数にシフト演算を行っても、正負の情報を保持できる。
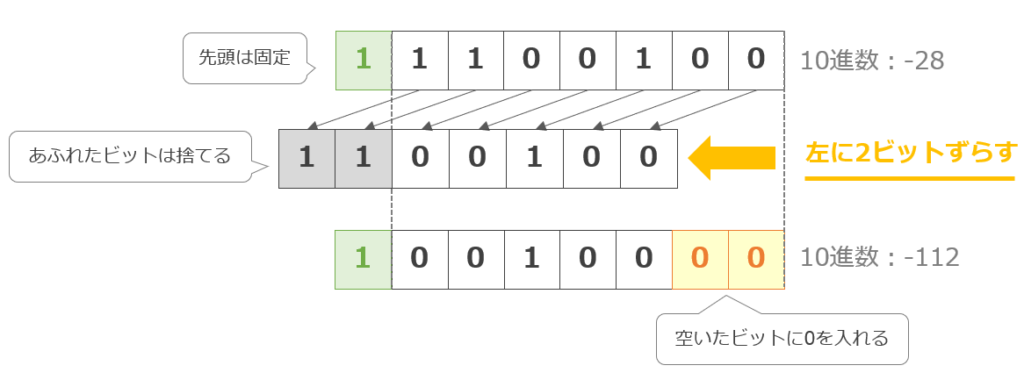
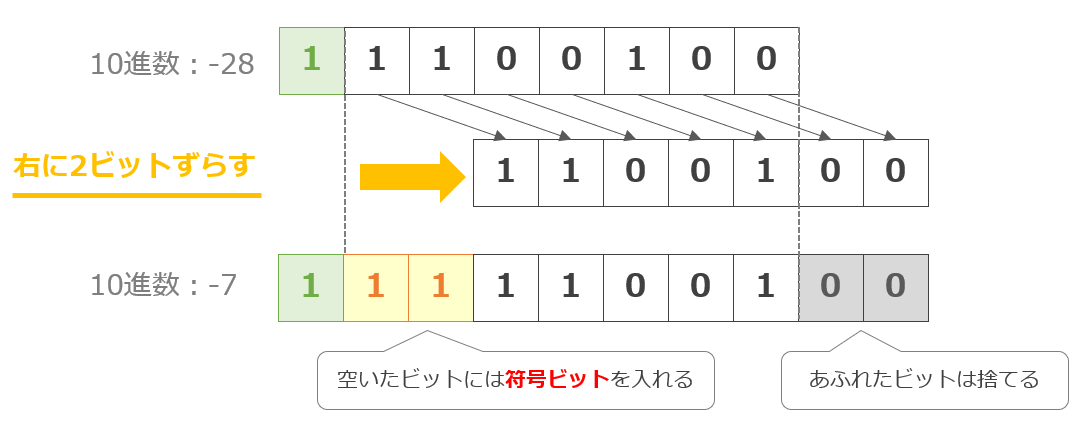
算術シフト演算の負の値は2の補数が使用されている。
・誤差
コンピュータでは、固定小数点数、浮動小数点数ともに有限のビットで2進数の各桁を表現するため、次のような誤差が発生する。
| 誤差 | 概要 | |
| 1 | 丸め誤差 | 切捨てや四捨五入で下位桁を削除して生じる |
| 2 | 桁落ち | 絶対値がほぼ等しい二つの数値について、異符号の加算や同符号の減算を行うことにより、有効桁数が減少する |
| 3 | 情報落ち | 絶対値の非常に大きな数値と小さな数値の演算を行った場合ん、小さな数値が無視される |
| 4 | 打切り誤差 | 無限に連続するような計算(円周率など)を有限の回数で打ち切るために生じる |
この他に、表現する値が表現可能な範囲よりも大きくなり、正しく表示や演算ができない現象をオーバーフロー(桁あふれ)というものもある。
また、浮動小数点演算において、表現する値が表現可能な範囲よりも小さくなり、正しく表示や演算できない現象をアンダーフローという。
後記
久しぶりの更新となった。
旧築地市場跡地は、ワクチンの接種会場となっていた。