私は高校生の頃数学が苦手で嫌いだった。嫌いだから不勉強になり、更に苦手になっていくという悪循環だった。
ただ振り返ってみて感じるのは、数学の勉強の仕方がよく分かってなかったのかなということだ。
今のようにインターネットや動画で検索できる時代でもなかった。
現代は情報過多かもしれないけど、とても便利な世の中になってきたなと思う。

コンピュータを学ぶ上でも、数学の素養は必須である。
今回は、コンピュータにおいて相当重要な分野である、論理演算と集合演算について観てみよう。
論理演算
ある条件があったとして、それが正しいか正しくないかを判断できるものを命題といい、正しいことを真(true)、正しくないことを偽(false)という。
また任意の命題を表す変数を論理変数(命題変数)という。
論理変数は真、偽のいずれかの値で表され、真と偽を1と0で表現することもある。これを真理値という。
論理変数を論理記号によって組み合わせたものを論理式という。
| 論理演算 | 意味 | 論理式の例 |
| 論理積(AND) | “かつ”を意味する。両方真だと真 | A・B |
| 論理和(OR) | “または”を意味する。少なくとも一つ真なら真 | A+B |
| 否定(NOT) | 論理変数が真なら偽、偽なら真 | ¬A 又は Ā |
| 排他的論理和(XOR) | 論理変数が異なれば真、同じだと偽 | A⊕B |
| 含意 | 論理変数Aが真ならBも真、Aが真でBが偽なら偽 | A →B |
各論理式の真理値を表形式で表現した真理値表は、以下のとおりだ。なお、1は真を、0は偽を表す。
| A | B | A・B | A+B | A⊕B | A→B | ¬A |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 1 | 0 |
論理式には基本公理というものがある。
論理変数A、B、Cの間では次の関係が成立する。
| 恒等則 | A・0=0 A・1=A A+0=A A+1=1 |
| 同一則 | A・A=A A+A=A |
| 交換則 | A・B=B・A A+B=B+A |
| 結合則 | A・(B・C)=(A・B)・C A+(B+C)=(A+B)+C |
| 分配則 | A・(B+C)=(A・B)+(A・C) A+(B・C)=(A+B)・(A+C) |
| 吸収則 | A・(A+B)=A A+(A・B)=A A・(Ā+B)=A・B A+(Ā・B)=A+B |
| 矛盾則 | A・Ā=0 |
| 排中則 | A+Ā=1 |
| 二重否定則 | ¬¬A=A |
| ド・モルガン則 | ¬(A・B)=¬A+¬B ¬(A+B)=¬A・¬B |
この表で一番重要なのは、ド・モルガン則である。
言語化すると、論理積の否定は否定の論理和に等しい、又は、論理和の否定は否定の論理積に等しい、ということになる。
論理式を簡略化するために用いる図にカルノー図というものがある。
論理変数のとりうる値を領域で表すとともに、隣接する領域を併合する。
最も上の行と最も下のは隣接しているとみなし、最も左の行と最も右の行も隣接しているとみなす。
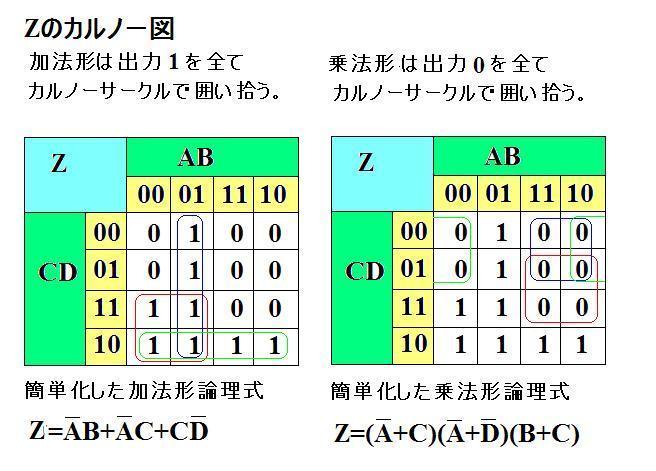
上図右側では、1(真)に着目している。
ABCDがどのような状態(0又は1)なら、1をとりうるかに注目である。
Aが0(偽)でかつBが1(真)ならCDが1でも0でも1になるため、左から2番目の縦の1の囲み部分は、Aの否定とBの論理積になる。
同じ要領で、左下の正方形の1のブロックは、Cが1かつAが0のとき1になるため、CとAの否定の論理積になる。
一番下の横軸の1のブロックは、Cが1でDが0のとき1になることから、CとDの否定の論理積になる。
Zが1になるのは、上記の3つのいずれかに該当すればよいのだから、Zは図の論理式になるのである。
論理式構築の要諦は、Zが1になるときのABCDで共通した部分を拾い上げることにある。
集合演算
集合とは、同じ属性をもつ要素の集まりである。
すべての要素を対象とした全体の範囲を全体集合という。
例えば、1以上10以下の整数を対象とした集合Sがあったとする。
全体集合は、
S={1,2,3,4,5,6,7,8,9,10}
となる。
このうち、偶数を集合Aとした場合、
A={2,4,6,8,10}
となる。
一方、その集合に含まれない要素からなる集合を補集合という。
Aの補集合をĀと表す場合、
Ā={1,3,5,7,9}
となる。
また、ある集合に対して、その集合の一部となる集合を部分集合という。
集合Bは集合Aの部分集合となり、B⊆Aのように表される。そして集合Aは全体集合Sの部分集合と考えることもできるので、B⊆A⊆Sとなる。
ベン図
集合を視覚的に分かりやすくする方法にベン図がある。
ベン図とは、各集合を円で表現する図のことである。

二つの集合を用いた集合演算には以下のものがある。
| 和集合 | A⋃B | 集合AとBのうち少なくとも一方に含まれる要素の集合 |
| 積集合 | A⋂B | 集合AとBに共通して含まれる要素の集合 |
| 差集合 | AーB | 集合AからBに含まれる要素を除いた集合 |
| 補集合 | Ā | 集合Aに含まれない要素の集合 |
これらをベン図で表すと分かりやすい。
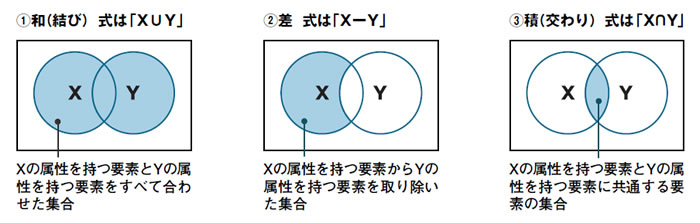

また、集合演算においても、論理式と同じような基本法則がある。
なお、ここでΦは要素が一つもない空集合を意味する。
| 交換の法則 | A⋂B=B⋂A A⋃B=B⋃A |
| 結合の法則 | A⋂(B⋂C)=(A⋂B)⋂C A⋃(B⋃C)=(A⋃B)⋃C |
| 分配の法則 | A⋂(B⋃C)=(A⋂B)⋃(A⋂C) A⋃(B⋂C)=(A⋃B)⋂(A⋃C) |
| 否定の法則 | A⋃Ā=S A⋂Ā=Φ ¬¬A=A |
| ド・モルガンの法則 | ¬(A⋂B)=¬A⋃¬B ¬(A⋃B)=¬A⋂¬B |
ここでも重要なのは、ド・モルガンの法則である。
集合演算においても、これを言語化していくと分かりやすい。

上図は例の一つであるが、私なりの言語化は、
AとBの積集合の否定はAの否定とBの否定の和集合に等しい。
AとBの和集合の否定はAの否定とBの否定の積集合に等しい。
ということになろう。
演算の応用
論理演算において、論理積の否定である否定論理積(NAND)と、論理和の否定である否定論理和(NOR)というのもある。
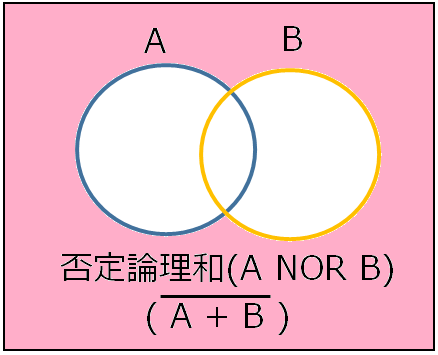
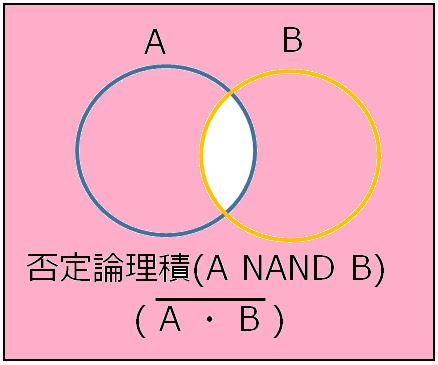
これらを使って、ちょっと数学めいた計算方法がある。
XとYの否定論理積X NAND Yは、NOT(X AND Y)とも表現できる。
これを利用して、X OR YをNANDだけ使って表すことができるのだ!
X OR Y
= NOT (NOT(X OR Y)) 二重の否定
=NOT((NOT X)AND(NOT Y)) ド・モルガン則
=(NOT X)NAND(NOT Y) NANDの定義
=NOT(X AND X) NAND NOT(Y AND Y)
=(X NAND X) NAND (Y NAND Y)
と変形できてしまうのだ。
ここでも、ド・モルガンの法則は登場してくる。
今回の例だと、論理和の否定は否定の論理積に等しいということだ。
また、否定の否定の二重否定も数学っぽい考え方だと思う。
後記
今回のブログ作成で一番苦戦したのは記号の入力だ。
どう入力すれば画面上に出せるのか分からず苦労したものである。
ITは便利だけど、慣れるまでは非常に大変だ(汗)