関係データベースにおいて重要なのが正規化理論である。
正規化とは、データの重複を排除して関連の強いデータを一つの表にまとめることにより、データの更新時異状(矛盾)の発生を抑制することである。
正規化は冗長性の排除と整合性の維持を目的とするのである。

・非正規形
複数の値をもつ繰り返し属性が含まれる表を、非正規形という。
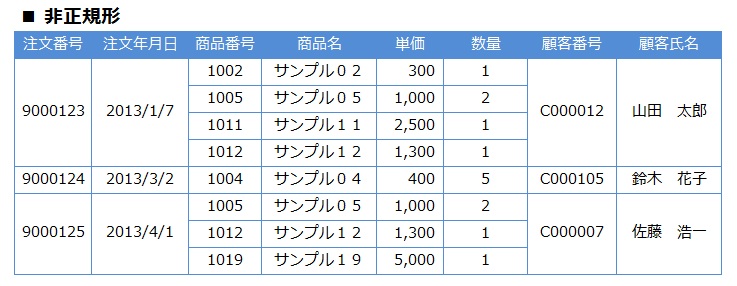
この例だと、1件の注文番号に対して複数の明細情報(商品番号、商品名など)が繰り返し属性として含まれるので非正規形となる。
非正規形の表は実装が困難なため、第1正規形に正規化する。
・第1正規形
表が繰り返し項目を含まない、表のすべてのドメインが単純であるような形式を、第1正規形という。
非正規形の繰り返し項目は異なる行として分離して、第1正規形に正規化する。

この表の主キーは、{受験番号、科目}となる。
受験番号だけでは安居氏の受けた2つの科目が区別できないからである。
第1正規形の表は正規度が低いため次のような問題点が生じる。
・行の追加ができないことがある。
受験科目の無い生徒の行を表に追加できない。
なぜなら”科目”は主キーに含まれており、非ナル制約が課せられているからだ。
・行の削除により情報が損失することがある。
安居氏が受験勉強に嫌気がさしてドロップアウトしたとき、”一流大学コース”の情報も失われる。
”一流大学コース”を受講しているのは安居氏だけだからである。
・値の更新によって矛盾が生じることがある。
”二流大学コース”を”中堅大学コース”と変更したとしよう。
この場合、整合性を保つためには、すべての行を正しく変更しないといけない。
このとき、1行でも変更し忘れたりすると、不整合(矛盾)が発生してしまう。
・第2正規形
第1正規形の正規度をさらに高めた形が第2正規形である。
第2正規形では関数従属性という概念が重要である。
属性集合X、Yの間に、Xの値が定まればYの値が一意に定まる、という関係があるとき、この関係を関数従属性という。
XはYに関数従属する(X→Y)という。
関係データベースでは、主キーの値が決まれば行を1つに特定できるので、すべての非キー項目は主キーに関数従属するといえる。
例:
*社員番号→氏名
社員番号が定まれば氏名は一意に定まる。
*氏名↛社員番号
社員番号は氏名に関数従属しない。同姓同名の社員いるなど。
また、X→Yという関数従属において、Xを構成するすべての項目がそろわないとYの値が一意に定まらないとき、YはXに完全関数従属するという。
主キーに完全関数従属しない項目が含まれるとき、このような関係は第2正規形では許されない。
第1正規形の表を第2正規形に正規化するということは、ある項目に完全関数従属するグループごとに分けるということである。
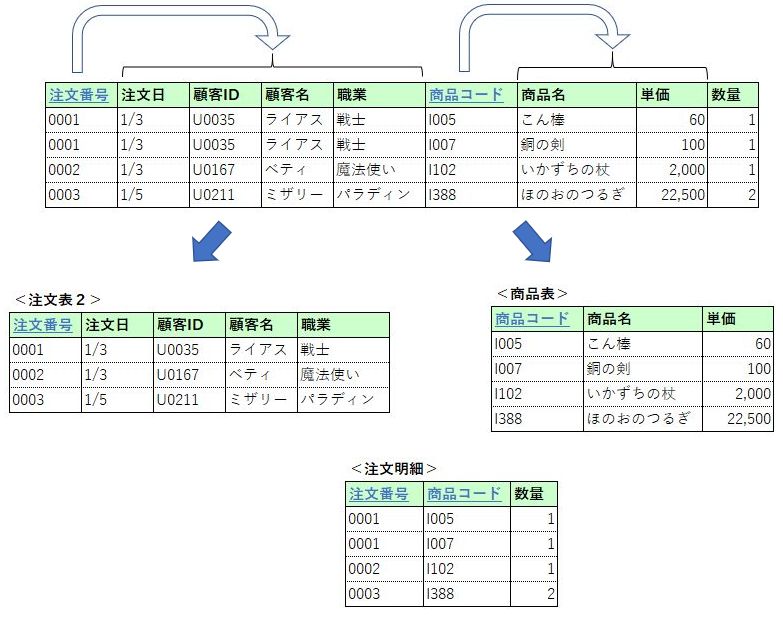
この表の例だと、注文番号のみに完全関数従属するのグループは、注文日・顧客ID・顧客名・職業、商品コードのみに完全関数従属するのは、商品名・単価、(注文番号・商品コード)に完全関数従属するのは数量ということだ。
まとめると、第2正規形は、すべての非キーが主キーに完全関数従属する(主キーの一部だけに関数従属する項目はない)ということである。
・第3正規形
第2正規形はさらに正規度をあげて、第3正規形にすることができる。
第3正規形とは、すべての非キーが主キーに推移的関数従属しないことを満たすということだ。
ここでは非キーどうしの関数従属性に着目していくことになる。
推移的関数従属とは、Xが定まればYが一意に定まり、Yが定まることによりZが一意に定まるという、二段階の関数従属性を指す。
(X→Y→Z) ZはXに推移的関数従属する。
X→YかつY→Z である。
推移的関数従属の、中継点となる属性集合Yは、分割後二つの表に重複させる。
Yは一方の表の主キーとなり他方の表の外部キーとなる。
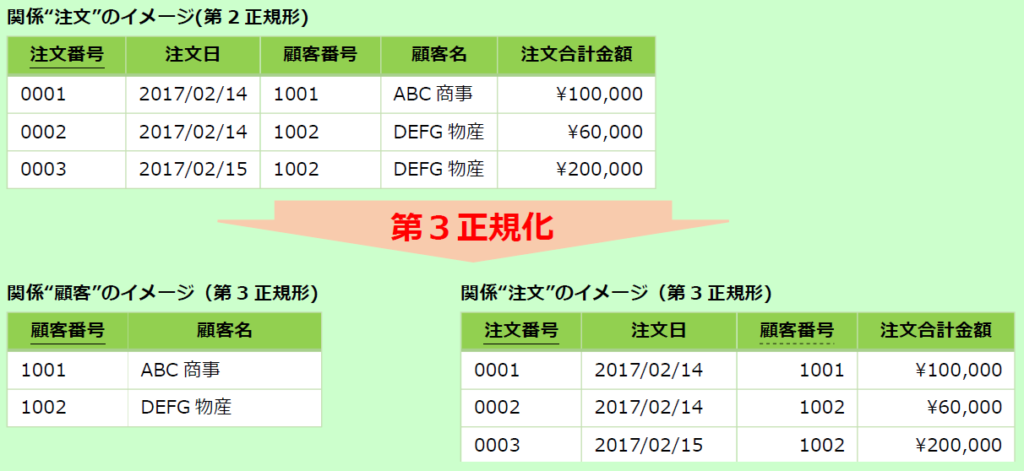
この表だと、顧客番号がYで顧客名がZに相当する。
第2正規形で残っていた問題点は、第3正規形に正規化することでほとんどが解決する。
注文表(右下の表)の行をすべて削除しても、顧客表(左下の表)の顧客に関する情報は残る。
また、顧客名は顧客表に記録されてるため、行ごとに顧客名が異なるという矛盾は生じない。
・正規化の長所と短所
正規化を行うことで、矛盾の生じにくい整理された表が得られる。
しかし、正規化は表の分割を伴うため、目的のデータを得るのに表の結合が生じ、応答性能が犠牲になることがある。
正規化の目的は、データの重複と矛盾の防止であると考えられる。
矛盾は行の追加や削除、更新により生じ、参照するだけでは生じない。
このため、更新される可能性が低く、主に参照に用いる表では、応答性能を優先するために正規度を低いままに保つこともある。
・後期
第1から第3までを簡単にまとめると、
第1 繰り返し項目無し。
第2 主キーに非キーは完全関数従属。
第3 非キーどうしの推移的関数従属排除。
というところだ。
要諦が分かったら、あとは多くの事例で学んでいけば、そう難しい話ではなさそうである。